復習備考

| 業(yè)務(wù)中心: | 0371-55696552 18037153049 |
您的當前位置:魯班培訓-一建培訓,二建培訓,監(jiān)理,注冊安全工程師等 > 復習備考 > 模擬試卷 >
利用平衡條件求未知力
作者:admin 來源:未知 瀏覽: 添加日期:2018-08-03
利用平衡條件求未知力
懸臂梁中的B點,即固定端支座,其支座反力為:
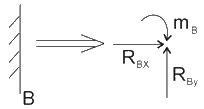 B點為固定支座
B點為固定支座 A點處為固定鉸支座,C點處為可動鉸支座
A點處為固定鉸支座,C點處為可動鉸支座簡支梁中的左側(cè)支座,即固定鉸支座,其支座反力為:
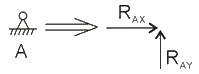
簡支梁中的右側(cè)支座,即可動鉸支座,其支座反力為:
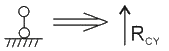
C
二、平衡方程
——ΣX=0
——ΣY=0
——ΣM=0
三、梁的內(nèi)力:剪力(V)、彎矩(M)
【典型考題】有一簡支梁受力與支承如下圖,則梁中的彎矩為( )kN.m。
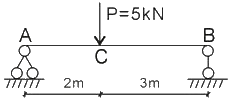
A.5
B.6
C.7.5
D.10
[答疑編號5683101201]
『正確答案』A
『答案解析』計算梁內(nèi)力的一般步驟:第一步,去掉約束,畫出桿件受力圖。假設(shè)A點處有向上的力RAY,水平的力RAX。
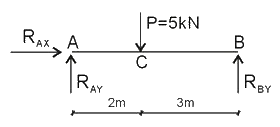
第二步:利用平衡方程,求出約束反力。
——ΣX=0 => RAX=0
——ΣY=0 => RAY+ RBY=5
——ΣMA=0 => 5×2=RBY×5=> RBY=2kN,RAY=3kN
第三步:如需計算梁的內(nèi)力(剪力或彎矩)可用截面法,取B點至跨中的一段梁作為隔離體,此時應(yīng)標注出跨中的內(nèi)力V跨中、M跨中,然后再列平衡方程,可以得出:跨中的彎矩= RBY *5/2=2×2.5=5KN.M
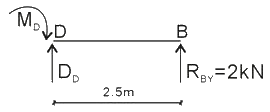
[2005年真題]有一伸臂梁受力及支承如圖,則固端A的彎矩為( )kN.m。
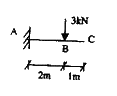
A.2
B.3
C.6
D.9
[答疑編號5683101202]
『正確答案』C
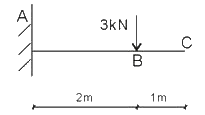
『答案解析』計算梁內(nèi)力的一般步驟:第一步,去掉約束,畫出桿件受力圖;
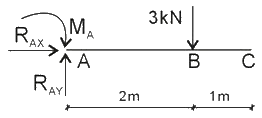
第二步:利用平衡方程,求出約束反力;
——ΣX=0=>RAX=0
——ΣY=0=>RAY=3kN
——ΣMA=0=>mA=3×2=6kN·m
第三步:用截面法計算出梁的內(nèi)力。如圖所示,固端A的彎矩=3×2=6KN.M
 鄭州
鄭州





